Normally when you work with your computer you don’t have to pay too much attention to its vital signs. Used system memory? No worries. Disk space? Mostly fine. CPU load? What even is that? As long as you don’t have some crappy HP laptop or a Chromebook, most modern laptops are fairly powerful and enable you to do whatever you want to without having to worry about anything becoming sluggish or overloading your computer.
Sometimes, however – or, rather: some people experience this – there are those programs that do pose very peculiar requirements to your computer. One genre of programs that do this is photo or video editing software. The other is programs you write for yourself. And both genres of programs pose these requirements for the very same reason: They work with large amounts of data.
When it comes to video or photo editing software, there is not that much you could do. For one, these programs are normally not Open Source, so you can’t improve their memory management even if you could. And then, if you reduce the amount of data these programs use, you directly reduce the amount of data of the stuff you’re working with, leading to less-than-ideal video or photo quality. And nobody wants that.
The second genre of programs, however – those you write yourself – have a big benefit: Even if you work with Gigabytes of data, you can actually reduce the memory footprint these programs have by a large margin without endangering your analyses. That, however, requires a lot of thought and skill.
Representing Data with Matrices
In the past, I never had to worry about the memory footprint of my programs, since most of them fall into the category of “regular stuff you can run on your computer,” like Zettlr. But ever since I started working on my PhD, the amount of data I have to work with increased by several magnitudes, and that leads to problems.
For starters, the current dataset I work with contains 30 GB of plain text. And since my computer has only 8 GB of memory, I can’t load in all of that at once.
However, for most of my analyses I can reduce the amount of data a lot. That is because you can represent words as numbers which take up much less space than the full text. This allows me to open one data file at a time, stream the data and immediately process it into a much smaller data structure. I have already written about how I do this in this article about a year ago, so I’m not going to repeat that here.
Rather, what I want to focus on for the remainder of this article is another kind of size problem of my data I ran into only a few days ago.
I am currently running a phalanx of analyses that treat my data as a so-called bag-of-words representation. That means, the algorithms only need info about whether some words are present in a document or not. This information is normally encoded in matrices.
Take the following example: Imagine you have four sentences:
- A first sentence.
- Twice as many!
- Thrice as many.
- A final sentence.
A list of all words occurring these sentences (a “vocabulary”) would be:
- a
- first
- sentence
- twice
- as
- many
- thrice
- final
Notice how we went from 12 words to just 8. Now what we would do is construct a so-called “document-term” matrix with four rows (one per sentence) and ten columns (one per unique word), and set each cell to a “1” if the document contains a given word, and “0” otherwise:
| a | first | sentence | twice | as | many | thrice | final | |
|---|---|---|---|---|---|---|---|---|
| Sentence 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| Sentence 2 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| Sentence 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| Sentence 4 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
Another sparse matrix that I eventually needed was a co-occurrence matrix, that is: A (symmetric) matrix that contains the amount of which words co-occur across the documents. The co-occurrence matrix of our four example sentences looks like this:
| a | first | sentence | twice | as | many | thrice | final | |
|---|---|---|---|---|---|---|---|---|
| a | 1 | 1 | 2 | 0 | 0 | 0 | 0 | 1 |
| first | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| sentence | 2 | 1 | 2 | 0 | 0 | 0 | 0 | 1 |
| twice | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| as | 0 | 0 | 0 | 1 | 2 | 2 | 1 | 0 |
| many | 0 | 0 | 0 | 1 | 2 | 2 | 1 | 0 |
| thrice | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| final | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
The matrix now looks differently, since it is quadratic and contains not just zeros and ones.
But why should we care? I worked with about 12,000 documents and about 15,000 unique words. All of that fitted into my memory, so no worries there. Then, however, I needed a larger sample and increased the amount of documents to 25,000, which in turn also increased my vocabulary size. And suddenly Python got the munchies and surpassed even Chrome in its memory demands:
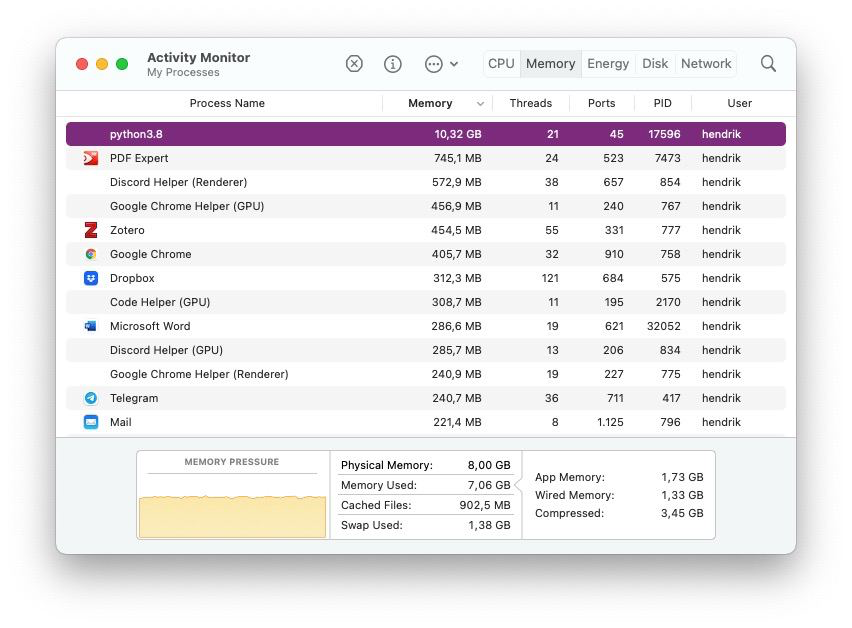
10 GB for just 25,000 documents that in total maybe use a few Megabyte of disk space?! A quick calculation on the document-term matrix confirmed my fears:
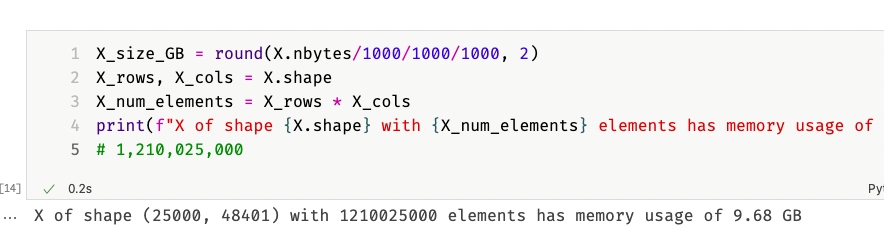
So a document-term matrix of 25,000×48,401 elements requires 10 GB of memory to store. That is too much, and it was palpable, because my computer became extremely sluggish. I was thinking about getting a new computer with more than 8 GB of memory. However, I quickly realized that even 32 GB would at some point be insufficient. In total, my dataset has roughly 17 million documents and about 6 million unique words. Such a matrix would have $17,000,000 * 6,000,000 = 102,000,000,000,000$ elements and, if we estimate one byte per element, the matrix would consume $\frac{102,000,000,000}{1,000,000,000} = 102 \text{GB}$ of memory.
Introducing Sparsity
This isn’t viable. But what should we do? Let us have another look at the matrices above. Mathematically, both matrices are “sparse” where sparse means that they contain many zeros.
And we can actually calculate a metric based on this information. This metric is called sparsity. It is calculated by simply taking the amount of zeros divided by the total number of elements in the matrix. For our document-term matrix, the sparsity is $\frac{20}{32} = 0.625$ or 62.5%. In other words: 62.5% of the matrix are empty! We can also calculate the sparsity for our co-occurrence matrix, which is $\frac{35}{64} = 0.55$ or 55%. Again, more than half of the cells in this matrix contain zeros.
Can we do something with this information? Yes, we can! If we think about these matrices, we query them for information. Right now, the question we always pose is “What number is the element at position (row, column)?” So if we call our document-term matrix $D$ and our co-occurrence matrix $C$, we could say that $D{i=3, j=2} = 0$ or that $C{i=3, j=1} = 2$.
However, we can rephrase the query question to our matrix. Instead we can ask “Is the element at position (row, column) a zero? If it is not, what number is it?” Now we are asking two questions instead of one. And this allows us to do something very smart algorithmically: Instead of saving every zero separately, we can combine that information in a way that our matrix knows “In row $i$ there are only zeros from column 423 to column 812.” This means that a sequence of 389 zeros (389 bytes) can be represented much smaller.
Density and Sparsity: Mathematics ≠ Algorithms
At this point, we should talk very briefly about sparse and dense matrices. In mathematics, a matrix is called dense if it contains a lot of different numbers and only a few zeros. If there are many zeros in the matrix, it is called sparse.
For a computer, however, a matrix is still dense even if it contains many zeros. Rather, for a computer a dense matrix is a data structure where each element is stored separately, whereas a sparse matrix is a matrix which stores only non-zero elements, and represents all zeros as ranges, rather than individual elements.
So while I was always working with sparse matrices, I stored them in my programs as dense matrices. Let’s quickly go back to the 9.6 GB matrix I had. I also calculated the sparsity for that matrix and, unlike our toy examples from above, the sparsity of the 25,000 documents-matrix was a whopping 99.9%!
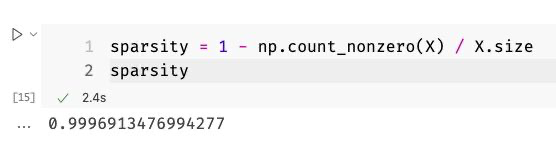
After I converted that monstrosity into a sparse matrix, the memory consumption of my Python process went down by a large margin! So let us have a quick look into how all of that works algorithmically to finish today’s article of!
Algorithms of Sparsity
In Python, if you work with anything even remotely mathematical, you normally refer to the library numpy. Numpy is cleverly designed from an algorithmic perspective and as such always allocates consistent blocks of memory. For example, a matrix with three rows and three columns would be stored in memory like this:
0x00 row 1 col 1
0x01 row 1 col 2
0x02 row 1 col 3
0x03 row 2 col 1
0x04 row 2 col 2
0x05 row 2 col 3
0x06 row 3 col 1
0x07 row 3 col 2
0x08 row 3 col 3If now somewhere in your code you query the matrix using matrix[2][2] what numpy would do is take the memory address of the very first element (0x00) and just add 2 to it (0x02) and then add another 2 to it (0x04) and return whatever is stored at that specific point in memory. This is equivalent to the first question from above, “What number is the element at position (row, column)?”
This makes accessing elements blazingly fast. For example, I can construct a co-occurrence matrix of size 48,000×48,000 in mere seconds. However, as you can imagine, since numpy stores each element separately, such a matrix can become extremely large extremely fast.
What would we need to change algorithmically to arrive at an equivalent of the second question, “Is the element at position (row, column) a zero? If it is not, what number is it?”? Instead of directly returning whatever is stored at the given memory location, we would first check if the queried element is zero, and if it is we can immediately return that. In pseudo-code that looks something like that:
def get_element (row, col):
# A sparse matrix contains a list of all
# cells that are *not* zero, which is
# faster to query if its sparsity is large.
if is_zero(row, col):
return 0
else:
return matrix[row][col]This does increase the computing cost by some margin, but if you have a sparse matrix, the wins in terms of size are absolutely worth it.
Caveats of Sparse Matrices
However, you can’t just create sparse matrices and be done with it. A sparse data matrix is extremely helpful in looking up information without having to store all of these zeros, but it does so at the expense of a very slow speed while constructing these matrices. For instance, if you use a sparse matrix and store new information in it, it needs to adapt the ranges which contain zeros, and that is much more expensive computationally than the regular approach by numpy to simply write something to an arbitrary memory location.
Remember that you can always turn the questions above around, and instead of asking what number a certain element is, you can also direct numpy to store information: “Store this number at index (row, column).” This is much faster if numpy exactly knows where it should put that number.
So how can we utilize both a fast writing speed and a fast reading speed? For that, it helps to remember that normally you construct data matrices once and then read them for the remainder of your program. That means, you just have to write to them once, and then read from them a lot.
Using Sparse Matrices
So here’s how you would use both dense and sparse matrices for a maximum of speed and a minimum of storage requirements. For sparse matrices I use SciPy, because numpy unfortunately doesn’t implement the necessary algorithms:
import numpy as np
from scipy.sparse import csr_matrix
# This is how our bag-of-words representation of the sentences looks like
documents = [
['a', 'first', 'sentence'],
['twice', 'as', 'many'],
['thrice', 'as', 'many'],
['a', 'final', 'sentence']
]
# Constructing a vocabulary as a dictionary makes lookups blazingly fast
vocab = {
'a': 0,
'first': 1,
'sentence': 2,
'twice': 3,
'as': 4,
'many': 5,
'thrice': 6,
'final': 7
}
# This creates a dense matrix where each element is stored separately
X = np.zeros((len(documents), len(vocab)), dtype=np.longlong)
for document_index, bow in enumerate(documents):
for word in bow:
if word in vocab:
# Storing something in X[i][j] takes exactly one CPU cycle
X[document_index][vocab[word]] = 1
# Here we are using SciPy's csr_matrix function to create a sparse
# matrix. There are more types of sparse matrices depending on your
# usecase. Have a look into the documentation!
# If X contains only 1% non-zero elements, the sparse matrix will take
# up maybe two or three percent of the size of X.
X_sparse = csr_matrix(X)
# At this point, the `del` operator comes in handy to explicitly remove
# the large X matrix and free up memory which we can then use for other
# computations -- like a topic model!
del XAs you can see, for a short amount of time we are indeed creating this 10 GB monstrosity. However, thanks to our operating system being really smart in how it swaps1 out the data that doesn’t fit into memory, we do this with just a moderate speed impairment. If we just construct one really large matrix at a time, this works fairly well.
-
Swapping basically means that it takes some data from your memory and writes this to your disk. Feel free to read my article on generators where I also explain what swapping is. ↩